| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 경사하강법
- 코딩테스트
- 정규화
- 인공지능 깃 버전관리
- API
- 의료 ai 대학원 월급
- 자바 영화 api
- 디자인패턴
- 머신러닝
- 딥러닝
- 로스트아크
- 백준
- MLP
- 통계학
- 자바 프로젝트
- 활성화 함수
- 대학원 월급
- pandas
- 파이썬 경사하강법
- 영화 api
- 자바
- 대학원 급여
- Dehaze
- python
- DCP
- C# 프로젝트
- 디자인 패턴
- 파이썬
- 딥러닝 실험 깃 버전관리
- 인공지능
- Today
- Total
대학원 일기
경사하강법(Gradient descent)(2) 본문
경사하강법(Gradient descent)
경사하강법 기반의 선형회귀 알고리즘
선형회귀 계수 구하기
선형회귀의 목적식은 $\left\| y-X\beta\right\|_{2}$이다. 이는 주어진 데이터에 대한 정답에 해당하는 $y$, 학습 데이터 $X$행렬에 가중치 $\beta$를 곱하여 두 벡터 값의 차이의 $L_{2} norm$을 최소화하는 가중치를 찾는 것이다.

$\beta$ 값을 최소화하기 위해서는 경사하강법 알고리즘을 적용하여 주어진 목적식을 $\beta$로 미분하고, 주어진 $\beta$에서 미분값을 빼주게 되면 최소값을 구할 수 있다.



목적식을 최소화하는 $\beta$를 구하는 경사하강법 알고리즘은 다음과 같다.





- 경사하강법 알고리즘은 loop를 통해 최적화하는 것이므로 적절한 학습률(learning late)와 학습횟수(parameter)를 잘 짜야한다.
확률적 경사하강법(stochastic gradient descent)
이론적으로 경사하강법은 미분 가능하고 볼록(convex)한 함수에 대해선 적절한 학습률과 학습횟수를 선택했을 때 수렴이 보장되어 있다. 특히 선형회귀의 경우, 목적식 $\left\| y-X\beta\right\|_{2}$은 회귀계수 $\beta$에 대해 볼록함수이기 때문에 알고리즘을 충분히 돌리면 수렴 되는 것을 보장할 수 있다.

위와 달리, 비선형 회귀 문제의 경우 목적식이 볼록하지 않을 수 있으므로 수렴이 항상 보장되지 않는다.

이를 해결하기 위해 확률적 경사하강법(stochastic gradient descent)을 이용한다.
확률적 경사하강법(stochastic gradient descent)
확률적 경사하강법(stochastic gradient descent)은 모든 데이터를 사용해서 업데이트하는 대신 데이터 한개 또는 일부 활용하여 업데이트한다.
볼록이 아닌(non-convex) 목적식은 SGD를 통해 최적화 할 수 있다.

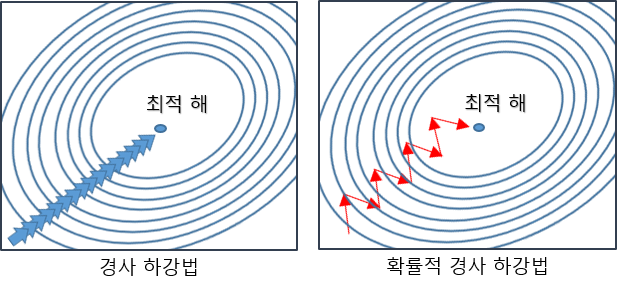
SGD는 데이터의 일부를 가지고 parameter를 업데이트하기 때문에 연산자원을 좀 더 효율적으로 활용하는데 도움이 된다.

확률적 경사하강법의 원리: 미니배치 연산
경사하강법은 전체데이터 $D = (x, y)$를 가지고 목적식의 그레디언트 벡터인 $\nabla_{\theta}L(D,\theta)$를 계산한다.

SGD는 미니배치 $D_{(b)}=(X_{(b)}, y_{(b)})\subset D$를 가지고 그레디언트 벡터를 계산한다. 미니배치는 확률적으로 선택하므로 목적식의 모양이 계속 바뀐다.
 |
 |

확률적 경사하강법의 원리: 하드웨어

- 만일 일반적인 경사하강법처럼 모든 데이터를 업로드하면 메모리가 부족하여 Out-of-memory가 발생한다.

- GPU에서 행렬 연산과 모델 패러미터를 업데이트하는 동안 CPU는 전처리와 GPU에서 업로드할 데이터를 준비한다.
'AI > 인공지능 기초' 카테고리의 다른 글
| 딥러닝(Deep learning) 학습 방법 (1) | 2022.02.01 |
|---|---|
| pandas(1) (0) | 2022.01.31 |
| 경사하강법(Gradient descent) (0) | 2022.01.27 |
| 행렬(Matrix) (0) | 2022.01.26 |
| 벡터(Vector) (0) | 2022.01.26 |




