| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 대학원 월급
- 대학원 급여
- 인공지능
- 영화 api
- 자바 프로젝트
- 통계학
- DCP
- 자바
- 머신러닝
- C# 프로젝트
- 로스트아크
- 디자인패턴
- 자바 영화 api
- 디자인 패턴
- Dehaze
- 경사하강법
- 의료 ai 대학원 월급
- 딥러닝 실험 깃 버전관리
- 백준
- pandas
- API
- 코딩테스트
- 활성화 함수
- 파이썬
- 딥러닝
- MLP
- 인공지능 깃 버전관리
- python
- 파이썬 경사하강법
- 정규화
- Today
- Total
대학원 일기
경사하강법(Gradient descent) 본문
경사하강법(Gradient descent)
미분의 개념과 그래디언트 벡터에 대해 설명합니다.
경사하강법의 알고리즘과 실제 코드에서의 구현을 보여줍니다.
접선의 기울기를 이용해서 함수의 최솟값으로 점을 이동시키는 원리를 알면 이를 바탕으로 경사하강법의 알고리즘과 수식을 이해할 수 있습니다.
특히 변수가 벡터인 경우, 편미분을 통해서 구한 그래디언트 벡터를 통해 d-차원으로 경사하강법을 확장할 수 있다는 개념을 확실하게 잡고 가시기 바랍니다.
미분(differentiation)이란?
미분(differentiation)
- 미분(differentiation)은 변수의 움직임에 따른 함수값의 변화를 측정하기 위한 도구로 최적화에서 가장 많이 사용되는 기법이다.

- 파이썬 sympy.diff로 미분 계산이 가능하다.

접선의 기울기
- 미분으로 함수 $f$의 주어진 점$(x, f(x))$에서의 접선의기울기를 구할 수 있다.

- 미분을 계산하려면 함수는 연속적(비선형)이어야 한다.
- 변화율 $\frac{f(x + h)-f(x)}{h}$의 $h$를 0으로 보내면 $(x, f(x))$에서 접선의 기울기로 수렴하게 된다.
접선의 기울기 부호(+/-)
- 접선에서 미분하여 기울기를 구할 때, 미분값이 양수라면 접하는 접선은 증가하는 함수이고, 미분값이 음수라면 접하는 접선은 감소하는 함수이다.
- 이를 통해, 한 점에서 접선의 기울기를 알면 어느 방향으로 점을 움직여야 함수값이 증가/감소하는 지 알 수 있다.
경사하강법(gradient descent)
경사 상승법(gradient ascent) / 경사하강법(gradient descent)
- 미분값을 더해줌으로써 함수값을 극대화 하는 것을 경사상승법(gradient ascent)이라고 한다.
- 미분값을 빼줌으로써 함수값을 극소화 하는 것을 경사하강법(gradient descent)이라고 한다.

- 경사상승/경사하강 방법은극값에 도달하면 움직임이 멈춘다.
- 극값에서는 미분값이 0이므로 더 이상 업데이트가 되지 않으므로 목적함수의 최적화가 끝나게 된다.

경사하강법 알고리즘

- 컴퓨터로 계산할 때 미분값이 0이 되는 것은 불가능하므로 eps보다 작을 때 종료하는 조건이 필요하다.
- var = var - lr * grad (주어진 변수 - 미분값)은 $x - \lambda f^{'}(x)$을 계산하는 부분이다. lr은 학습률로써 미분을 통해 업데이트 하는 속도를 조절한다.(학습률을 다룰 때에는 조심히 다루어야 함)
- 종료조건이 성립하기 전까지 미분값을 계속 업데이트한다.

경사하강법에서 다루는 변수가 벡터(vector)나 행렬(matrix)일 경우 = 편미분
- 벡터는 n차원 공간에서 계산되는 한 점이기 때문에 이동을 할 때 많은 방향을 가지게 된다. 이 경우, 미분을 특정 방향의 좌표축으로 이동하는 형식으로 정의할 수 있는데 이를 편미분(partial differentiation)이라고 부른다.

- 편미분 공식에서 $e_{i}$라는 벡터는 주어진 벡터 $x$가 있을 때 $x$의 $i$번째에 벡터에만 영향을 주고 나머지에는 영향을 주지 않는 단위벡터이다.
단위벡터: $i$ 번째 벡터값만 1이고 나머지는 0인 벡터
- 단위벡터를 이용하면 i번째 변수에서만 변화율을 계산하여 경사하강법 알고리즘을 사용할 수 있다.
정리: 변수가 벡터인 경우에도 편미분을 통해 경사하강법을 사용할 수 있다.
 |
 |
- 위 식과 코드를 보면 $x$ 방향에서 편미분한 것을 확인할 수 있다. → $x$ 방향의 움직임만 계산
그레디언트(gradient) 벡터
- 각 변수 별로 편미분을 계산한 그레디언트(gradient) 벡터를 이용하여 경사하강/경사상승법에 사용 할 수 있다.

- 일반적인 d차원 공간에서 벡터에 적용되는 경사하강법을 똑같이 구현할 수 있다.
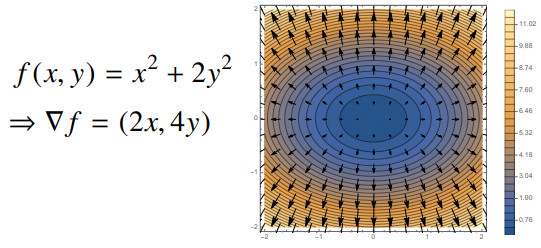
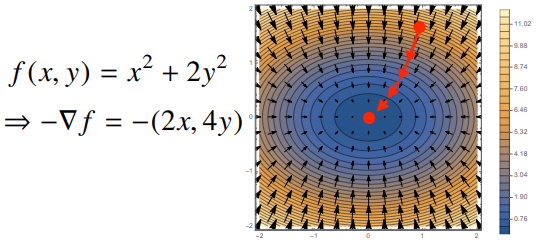
- 각 점 $(x, y, z)$ 공간에서 $f(x, y)$ 표면을 따라 $-\nabla f$ 벡터를 그리면 아래와 같이 그려진다

 |
 |
 |
 |
벡터에서의 경사하강법 알고리즘

- 함수가$f(x) = x^{2} +2y^{2}$ 일때 경사하강법으로 최소점을 찾는 코드

'AI > 인공지능 기초' 카테고리의 다른 글
| pandas(1) (0) | 2022.01.31 |
|---|---|
| 경사하강법(Gradient descent)(2) (0) | 2022.01.29 |
| 행렬(Matrix) (0) | 2022.01.26 |
| 벡터(Vector) (0) | 2022.01.26 |
| Numerical Python - Numpy (0) | 2022.01.25 |




