| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- python
- pandas
- 디자인 패턴
- 대학원 월급
- 대학원 급여
- 코딩테스트
- 딥러닝
- 딥러닝 실험 깃 버전관리
- 디자인패턴
- 백준
- 자바 영화 api
- 영화 api
- C# 프로젝트
- API
- 파이썬
- 정규화
- 의료 ai 대학원 월급
- Dehaze
- 인공지능 깃 버전관리
- 활성화 함수
- 경사하강법
- 머신러닝
- MLP
- 통계학
- 로스트아크
- 파이썬 경사하강법
- 자바
- DCP
- 자바 프로젝트
- 인공지능
- Today
- Total
대학원 일기
벡터(Vector) 본문
벡터(Vector)
벡터(Vector)란?
벡터(Vector)
- 벡터는 숫자를 원소로 가지는 리스트(list) 또는 배열(array)이다.

- 파이썬에서 벡터를 표현할 때는 주로 numpy를 사용한다.

- 행벡터: 가로로 배열
- 열벡터: 세로로 배열
벡터란?
- 벡터는 공간에서 한 점을 나타낸다.
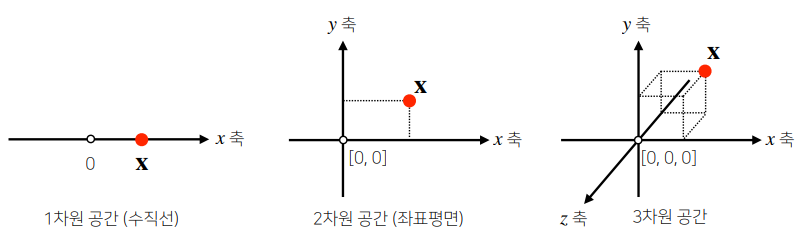
- 인공지능에서 다루는 벡터는 훨씬 더 큰 n차원의 공간으로 보통 n개의 축을 가지는 좌표 평면 내에서 표현되는 점이라고 이해하면 된다.
- 벡터는 원점으로부터 상대적 위치를 표현한다.


- 벡터끼리 같은 모양을 가지면 덧셈, 뺄셈, 성분곱(Hadamardproduct, element wise product) 등을 할 수 있다.
 |
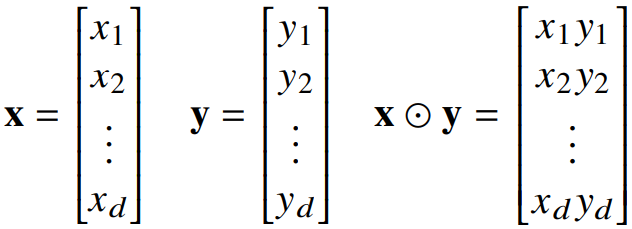 |
- numpy를 통해 코드로 구현할 수 있다.

벡터의 덧셈
- 벡터는 공간에서 한 점을 나타낸다.
- 벡터는 원점으로부터 상대적 위치를 표현한다.
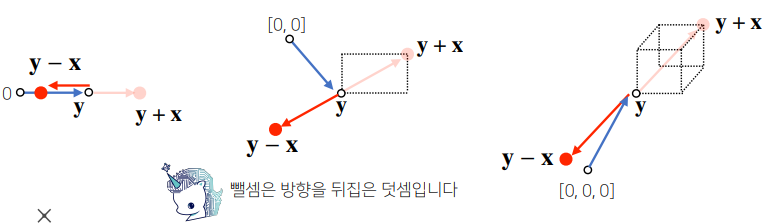
- 두 벡터의 덧셈은 다른 벡터로부터 상대적 위치 이동을 표현한다.

벡터의 뺄셈
- 벡터의 뺄셈은 벡터의 덧셈의 방향을 뒤집은 것
벡터의 노름(norm)
norm
- 벡터의 노름(norm)은 원점에서부터의 거리를 말한다.

$L_{1}$ $norm$
: $L_{1}$ - $norm$은 각 성분의 변화량의 절대값을 모두 더한다.
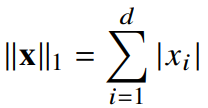 |
 |
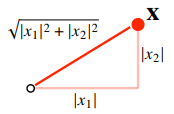
$L_{2}$ $norm$
: $L_{2}$ - $norm$은 피타고라스 정리를 이용해 유클리드 거리를 계산한다.
 |
 |

$L_{1}$ $norm$과 $L_{2}$ $norm$의 차이
- 노름의 종류에 따라 기하학적 성질이 다르다.
- 머신러닝에서는 각 성질들이 필요할 때가 있으므로 둘 다 사용한다.

두 벡터 사이의 거리 & 각도
두 벡터 사이의 거리
- $L_{1}$, $L_{2}$ $norm$을 통해 두 벡터 사이의 거리를 계산할 수 있다.
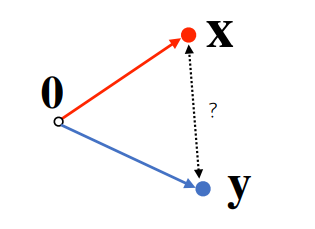
- 두 벡터 사이의 거리를 계산할 때는 벡터의 뺄셈을 이용한다.(이 때, 뺄셈을 거꾸로 해도 거리는 같음)
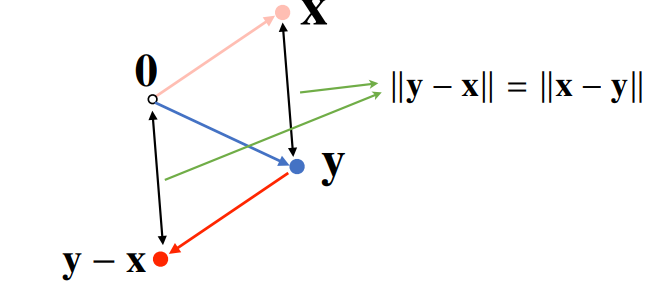
두 벡터 사이의 각도
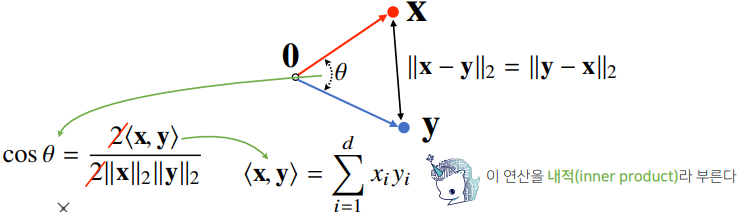
- 제2 코사인(cos) 법칙을 통해 두 벡터 사이의 각도를 계산할 수 있다.($L_{2}$ $norm$을 사용)
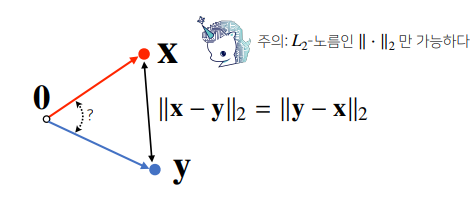 |
 |
- 위 오른쪽 사진에서의 분자를 내적으로 나타낼 수 있다.

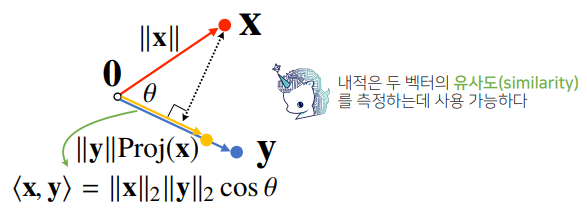
내적(inner product)의 해석
- 내적은 정사영(orthogonalprojection)된 벡터의 길이와 관련이 있다.
- Proj(x)의 길이는 코사인 법칙에 의해 $\left| \left| x\right|\right| cos \theta $가 된다.

- 내적은 정사영의 길이를 벡터$y$의 길이$\left| y\right|$만큼 조정한 값이다.
'AI > 인공지능 기초' 카테고리의 다른 글
| 경사하강법(Gradient descent) (0) | 2022.01.27 |
|---|---|
| 행렬(Matrix) (0) | 2022.01.26 |
| Numerical Python - Numpy (0) | 2022.01.25 |
| [DL] Deep Learning, Historical Review (0) | 2022.01.07 |
| 기계 학습(Machine Learning) (0) | 2022.01.02 |




