| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 코딩테스트
- 디자인 패턴
- 대학원 월급
- 자바
- 대학원 급여
- 머신러닝
- 딥러닝
- 디자인패턴
- 자바 프로젝트
- API
- 통계학
- 경사하강법
- DCP
- 의료 ai 대학원 월급
- 딥러닝 실험 깃 버전관리
- 영화 api
- 활성화 함수
- 인공지능 깃 버전관리
- 파이썬
- 인공지능
- Dehaze
- 로스트아크
- 백준
- 파이썬 경사하강법
- python
- pandas
- MLP
- 정규화
- C# 프로젝트
- 자바 영화 api
- Today
- Total
대학원 일기
[논문 리뷰] A Fast Single Image Haze Removal Algorithm Using Color Attenuation Prior(CAP) 본문
[논문 리뷰] A Fast Single Image Haze Removal Algorithm Using Color Attenuation Prior(CAP)
대학원생(노예) 2022. 2. 15. 04:23
이 논문은 Color Attenuation Prior(이하 CAP)라는 기법으로 안개를 제거한다. CAP 기법은 안개 영상의 깊이 정보를 구해 안개제거 영상을 얻는 방법이다. 이를 위해, 안개 영상의 깊이를 모델링하기 위한 선형모델을 만들고, 지도학습으로 모델의 모수(매개변수, parameter)를 학습하여 깊이 정보를 recover 하여 안개가 제거된 깨끗한 영상을 얻는다.
아래의 링크를 통해 논문은 확인할 수 있다.
A Fast Single Image Haze Removal Algorithm Using Color Attenuation Prior
Single image haze removal has been a challenging problem due to its ill-posed nature. In this paper, we propose a simple but powerful color attenuation prior for haze removal from a single input hazy image. By creating a linear model for modeling the scene
ieeexplore.ieee.org
1. Introduction
실제 영상을 통해 돌아가는 시스템들 중 나쁜 날씨(안개)로 인해 저하된 이미지로 수행하는 경우 정상적으로 작동되지 않는 경우가 있다. 이 문제를 해결하여 기존 안개제거 알고리즘을 개선해 다양한 분야에서 도움이 될 것이라고 한다.
초기의 안개제거 알고리즘인 히스토그램을 기반으로한 안개제거 기술(histogram-based dehazing method)은 단일 이미지를 다뤘으나, 하나의 안개 이미지는 많은 정보를 얻기에 제한적이여서 이후 다중의 이미지를 사용하는 polarization-based method가 나오게 되었다. 이후에 Narasimhan이 제안한 안개제거 접근방식을 이용하여 DCP가 나온 후, 깊이 정보를 이용한 안개제거가 나온다. 논문에서 설명하는 다른 기법들(MRF, ICA, DCP)은 생략하겠다.
논문에서 제안하는 Color Attenuation Prior(이하 CAP)는 단일 이미지의 안개제거 방법이다. 이 방법은 지도학습(supervised learning)으로 안개 영상의 깊이에 대한 선형 모델을 학습시켜 복구된 깊이 정보로 안개를 제거한다. 이에 대한 결과는 다음 사진(Fig.1)과 같다.

2. Atmospheric Scattering Model
Atmospheric Scattering Model(대기 산란 모델)은 이전 글에서도 올렸듯이 안개제거 관련 논문에서 꼭 다루는 내용이다. 대기 산란 모델은 아래 사진을 보고 안개제거 모델식과 비교하면 쉽게 이해할 수 있다.
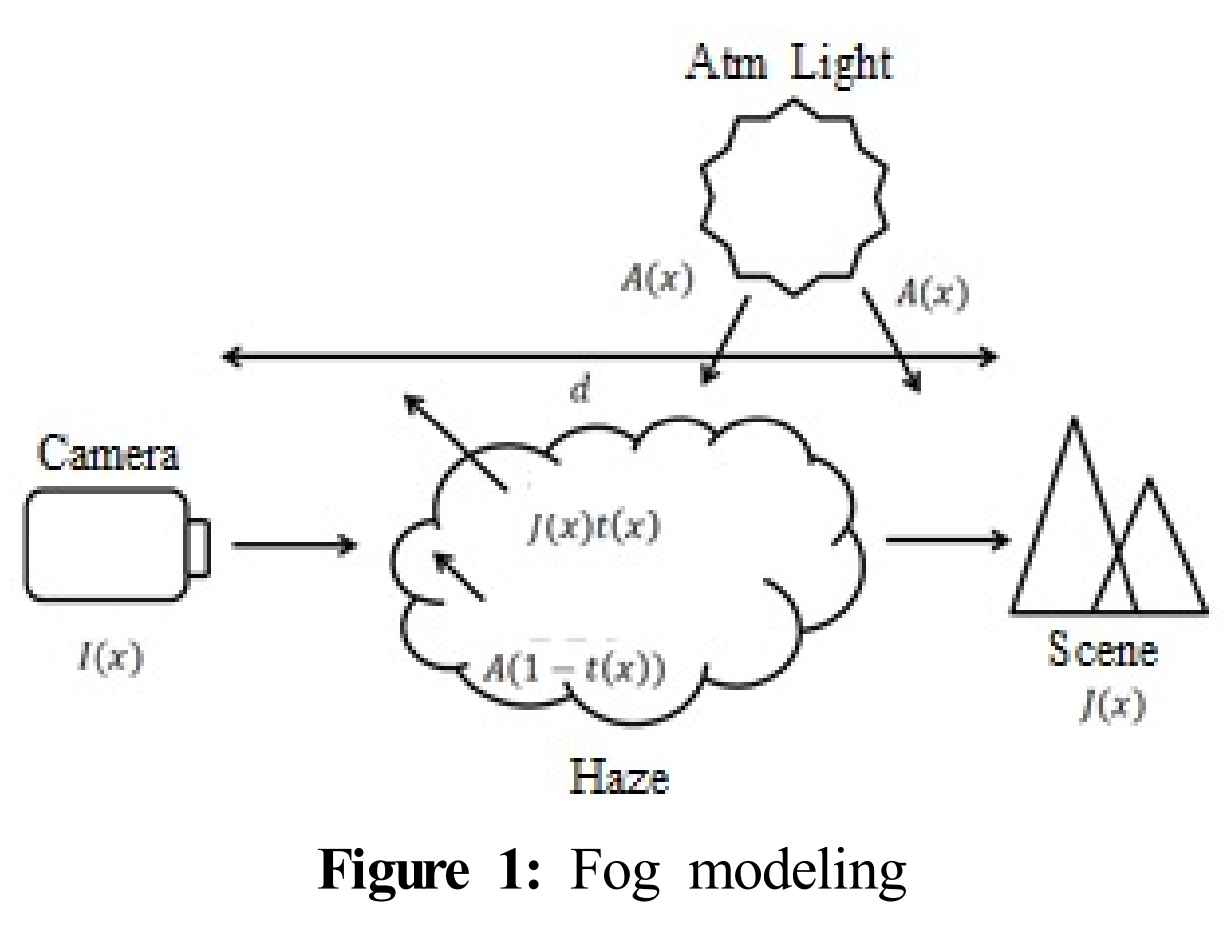
안개제거 모델식: $I(x) = J(x)t(x)+A(1-t(x))$
$t(x) = e^{-\beta d(x)}$
- $I(x)$ : 안개가 포함된 영상
- $J(x)$ : 안개가 존재하지 않는 깨끗한 영상
- $A$ : 안개 입자에 의해 산란되는 빛으로 인해 변질되는 영상의 정도(전역대기 산란광 또는 안개값)
- $e^{-\beta \times d(x)}$ : 최종적으로 산란되지 않고 카메라로 전달된 양(전달량, $t(x)$로 치환하여 사용)
- $\beta$ : 대기 산란 계수(Atmospheric Scattering Coefficient)
- $d(x)$ : $x$ 위치에서의 카메라와 대상 간 거리, 영상의 깊이(depth)
3. Color Attenuation Prior
단일 안개 영상에서 깊이 정보를 복원하는데 유용한 color attenuation에 대해 설명한다.
논문에서 사람의 뇌는 부가적인 정보 없이도 안개가 있는 부분을 빠르게 식별할 수 있다는 점을 보고, 논문의 저자는 안개 영상에서 화소의 밝기(value)와 채도(saturation)가 안개의 정도에 따라 달라진다는 것을 발견했다.
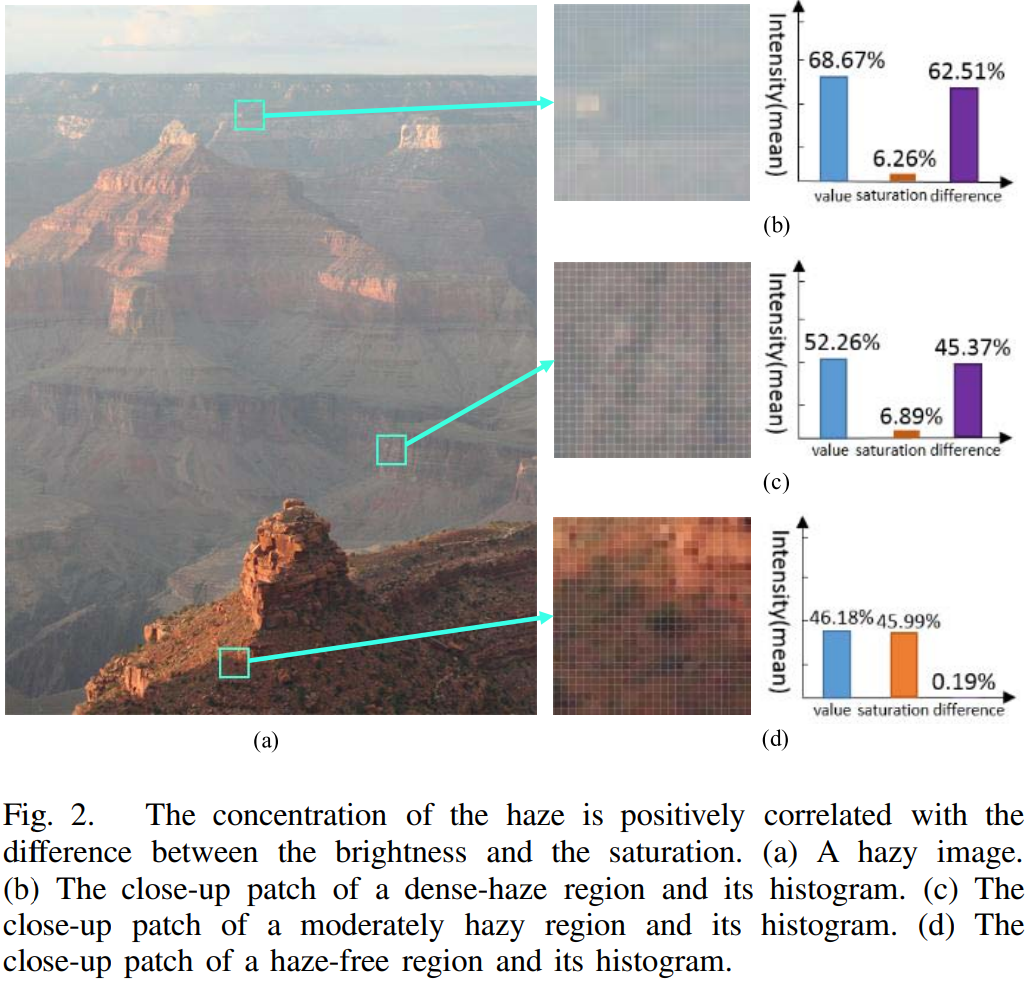
Fig.2는 저자가 발견한 정보들을 나타낸 것이다. 안개가 있는 (a) 영상을 (b), (c), (d) 영역으로 나누어 화소의 밝기(value)와 채도(saturation)를 조사하였다.
- (b)는 안개가 밀집된 영역으로 안개로 인해 밝기가 높게 나오고 채도는 낮게 나오면서 밝기와 채도의 차이가 크게 나타났다.
- (c)는 안개 정도가 중간 정도이며 안개로 인해 밝기가 52.26%이고, 채도는 낮게 나오면서 (b)와 마찬가지로 밝기와 채도의 차이가 크게 나타났다.
여기서 주목해야 한다.
- (d)는 맑은 깨끗한 영역으로 밝기(value)와 채도(saturation)의 값이 비슷하여 밝기와 채도의 차이가 작게 나타났다.
즉, 안개가 없는 영역에서는 채도가 높으며 밝기와 채도의 차이가 별로 없고, 안개가 있는 영역은 채도가 낮으며 밝기와 채도의 차이가 크다는 것을 알 수 있다. 이를 통해, 본 논문은 화소의 밝기(value)와 채도(saturation) 그리고 밝기와 채도의 차이(difference)에 주목하고, 이는 CAP에서 보는 3가지 특성이 된다.

Fig.3의 왼쪽 사진은 imaging system에 따른 안개가 없는 선명한 영역이고, 오른쪽 사진은 imaging system에 따른 안개가 낀 영역이다. 논문에서는 안개가 있는 영역에는 두 가지 메커니즘이 있다고 한다. 이는 대기 산란광(Airlight)과 직접 감쇠(Direct attenuation)으로 안개모델식의 안개가 있는 영상 $
안개제거 모델식: $I(x) = J(x)t(x)+A(1-t(x))$
위 식의 $J(x)t(x)$ 부분이 직접감쇠(Direct attenuation)로 곱셈 방식으로 감소한다. 이를 보고, 햇빛으로 인해 밝기는 증가(enhance)되고, 채도는 감소(reduce)되는 것을 알 수 있다. 즉, 안개의 정도에 따라 Pixel의 intensity(강도)가 약해지고 곱셈 방식으로 감소한다.
$A(1-t(x))$는 대기산란광(Airlight)으로, 대기산란광이 클수록 밝기는 증가하는 반면에 채도는 감소한다. 대부분의 경우에서 대기산란광이 더 중요한 역할을 하므로 영상의 안개 영역은 높은 밝기(value)와 낮은 채도(saturation)를 특징으로 한다. Fig.2에서 확인할 수 있듯이 안개가 짙을수록 대기산란광의 영향력은 커진다.
위 정보를 통해 밝기와 채도의 차이를 이용하여 안개의 정도를 추정할 수 있다. Fig.4는 안개의 정도에 따라 밝기(value)와 채도(saturation)의 차이가 증가함을 보여준다.

Fig.4처럼 안개의 정도를 추정하면서 깊이를 파악할 수 있고, 안개의 정도와 영상의 깊이가 상관관계를 가지고 선형관계에 있다고 볼 수 있다. 본 논문에서는 이러한 관계를 다음과 같이 정의한다.
$d(x) \propto c(x) \propto v(x) - s(x)$
- $d(x)$: 영상의 깊이
- $c(x)$: 안개의 정도(concentaration of the haze)
- $v(x)$: 화소의 밝기(value)
- $s(x)$: 화소의 채도(saturation)
- $v(x) - s(x)$: 밝기와 채도의 차이(difference)

Fig.5의 (a)는 HSV(Hue, Saturation, Value) 모델이고 (b), (c), (d)는 각각 근거리, 중거리, 원거리에 따른 장면 깊이를 HSV형태로 나타낸 것이다. (b), (c), (d)를 자세하게 들어가보면 벡터 $I(x)$ 안개 영상이고, 높이는 밝기(value)이고, 평면 원은 채도(saturation) 그리고 평면과 벡터 $I$의 각도를 $\alpha$라고 한다. Fig.5의 (b), (c), (d)를 보면 $\alpha$의 값이 0˚~90˚ 사이에서 변화할 때, $\alpha$의 값이 클수록, 접선의 기울기가 더 커지고, $V$ 방향의 $I$ 성분과 $S$ 방향의 $I$ 성분 간의 차이 또한 커진다. 즉, 깊이가 증가함에 따라 $v$ 값은 증가하고 $s$는 감소하는 것을 볼 수 있다.
(벡터 $I(x)$를 value 방향으로 정사영한 값과 saturation 방향으로 정사영한 값의 차이가 클수록 각도 $\alpha$가 크다)
4. Scene Depth Restoration(영상 깊이 복원)
A. The Linear Model Definition
위에서 정의한 내용을 토대로 밝기와 채도의 차이(difference between brightness and saturation)와 안개의 정도는 선형관계에 있다는 것을 알 수 있었다. 즉, 안개 영상의 깊이와 선형관계가 있다는 것이다. 이를 통해, 저자들은 선형모델을 만들었고, 더 적절한 표현으로 나타내었다. 이는 다음과 같다.
$d(x) = \theta_{0} + \theta_{1}v(x) + \theta_{2}s(x) + \varepsilon(x)$
여기서 $x$는 영상에서의 위치이고, $d$는 영상의 깊이이고, $v$와 $s$는 각각 밝기와 채도이다. $\theta_{0}, \theta_{1}, \theta_{2}$은 알려지지 않은 선형계수이다. $\varepsilon(x)$는 모델의 랜덤 오차이다. 저자들은 위 식을 가우시안(정규분포)로 나타낸다.

이어서 위 식을 편미분하면 다음과 같다.
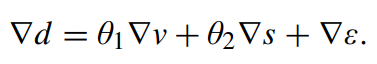

Fig.6는 안개 영상의 edge를 나타내는 것으로 CAP가 edge를 보존하는데 탁월한 것을 볼 수 있다. Fig.6의 (a)는 input되는 안개 영상이고, (b)는 (a)를 Sobel 커널을 적용한 영상이고, (c)는 Sobel 커널을 적용한 (b)를 $\theta_{1}$를 1.0, $\theta_{2}$를 -1.0으로 하여 편미분된 식을 적용한 것이다. (d)는 (e)에 Sobel 커널을 적용한 것으로 (e)는 표준편차가 0.05일 때의 랜덤 이미지 $\varepsilon$으로 매우 어둡게 나타난다. 이는 깊이(d)의 edge 분포는 작은 표준편차일 때 $\varepsilon$와는 독립적인(무관한) 것을 알 수 있다. 이를 통해, 다시 한 번 선형관계 있다는 것을 확인할 수 있다.
B. Training Data Collection
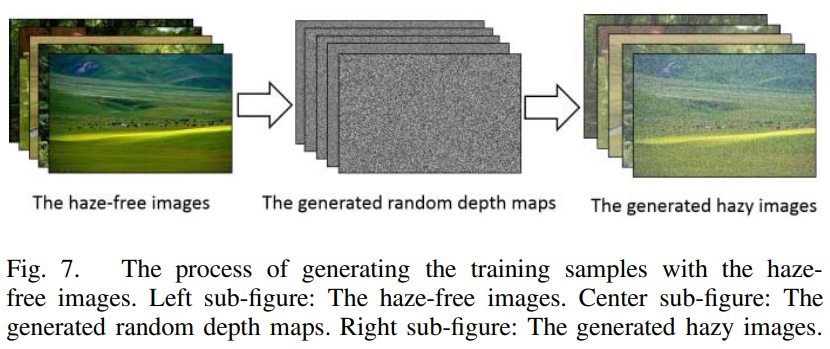
CAP를 구현하기 위해서는 위에 편미분한 식에서 $\theta_{0}$, $\theta_{1}$, $\theta_{2}$ 계수를 학습(learn)해야 한다. 본 논문에서는 계수들을 학습하기 위해 안개 영상과 깊이지도로 훈련(train)한다. 학습 이미지들은 Fig.7처럼 구글의 안개가 없는 맑은 영상에 랜덤으로 생성한 깊이지도를 적용하여 500개의 안개 영상을 얻는다.
C. Learning Strategy
본 논문에서 CAP는 다음과 같은 학습 전략을 통해 구현한다.
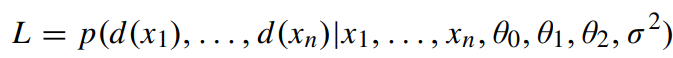
- $L$: 가능도
- $d(x_{n})$: n번째 scene point의 깊이
- $d(x) = \theta_{0}+\theta_{1} v(x)+\theta_{2} s(x) + \sigma(x)$
위 식의 $p(d(x_{1}) ~ d(x_{n}))$는 누적 곱 연산으로 나타내어 아래 식처럼 간단히 정리할 수 있다.

정리한 식의 $p(d(x_{i}))$는 정규분포로 나타낼 수 있으므로 다음과 같은 식이 나온다.
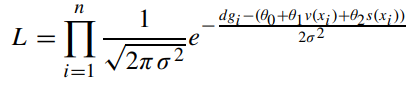
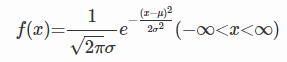
정규분포로 나타낸 식에서 $dg_{i}$는 장면에 대한 깊이를 의미한다. 정규분포로 정리한 식으로 $L$의 최대값을 구하기 위해 최대 가능도 방법을 이용한다. 본 논문의 식에서는 자연로그를 취한 $L$에 arg max를 하여 $L$의 최대값을 구하기 위한 $\theta_{0}, \theta_{1}, \theta_{2}$ 값과 $\sigma$를 구한다.
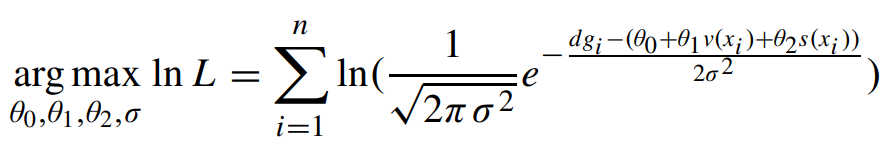
위 식을 $\sigma$로 편미분하고 0과 같게 한다.
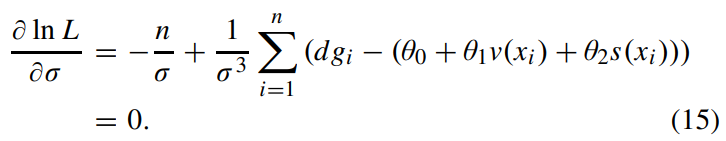
이 후 $\sigma^{2}$에 대한 식으로 나타내면 다음 식과 같다. 아래 식은 그냥 위 식을 이항정리와 정리만 하면 나온다.
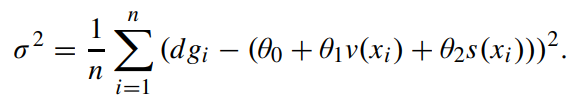
위 식을 통해 경사하강법 알고리즘을 적용하여 $\theta_{0}, \theta_{1}, \theta_{2}$ 각각 편미분 해주면 다음과 같다.
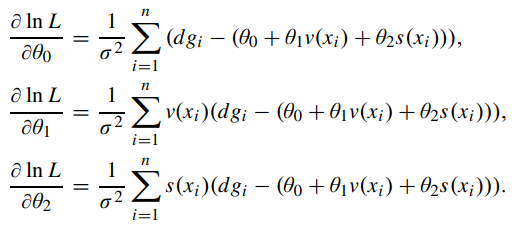
이처럼 $\theta_{0}, \theta_{1}, \theta_{2}$ 계수를 학습하여 알아냄으로써 보다 나은 안개제거 영상을 얻을 수 있다.
이에 대한 코드와 더 자세한 내용들은 논문을 직접 보기 바란다.
6. Experiments






