| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 인공지능
- API
- 파이썬 경사하강법
- 딥러닝
- 자바
- 활성화 함수
- 통계학
- C# 프로젝트
- 정규화
- 영화 api
- 로스트아크
- 파이썬
- Dehaze
- 디자인패턴
- MLP
- 대학원 월급
- 인공지능 깃 버전관리
- 경사하강법
- pandas
- 머신러닝
- 자바 프로젝트
- 자바 영화 api
- DCP
- 코딩테스트
- 디자인 패턴
- 의료 ai 대학원 월급
- 백준
- 대학원 급여
- python
- 딥러닝 실험 깃 버전관리
- Today
- Total
대학원 일기
케라스 창시자에게 배우는 딥러닝 2장 본문
2. 신경망의 수학적 구성요소
2.1 신경망과의 첫 만남
본 장에서는 MNIST 데이터셋으로 사용하여 손글씨를 분류하는 문제를 다룹니다.

케라스에서 MNIST 데이터셋 적재하기
데이터셋 로드
from tensorflow.keras.datasets import mnist
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()train_images, train_labels에 훈련셋을 담고, test_images, test_labels에 테스트셋을 담습니다.
mnist를 로드하면 (train 이미지, train 레이블), (test 이미지, test 레이블)로 불러옵니다.
이미지는 넘파이(numpy) 배열로 인코딩되어 있고 레이블은 0부터 9까지의 숫자 배열이다. 이미지와 레이블은 1대1 관계를 가집니다.
훈련 데이터, 테스트 데이터 확인
print("train image shape: ", train_images.shape)
print("train label length: ", len(train_labels))
print("train label: ", train_labels)
print("test image shape: ", test_images.shape)
print("test label length: ", len(test_labels))
print("test label: ", test_labels)
train set은 60000개의 이미지가 있고, 이미지 사이즈가 28x28 입니다.
test set은 10000개의 이미지가 있고, 이미지 사이즈는 동일합니다.
신경망 구조
신경망의 핵심 구성 요소는 층(layer)입니다. layer는 주어진 문제에 더 의미있는 표현(representation)을 입력된 데이터로부터 추출합니다. 즉, 딥러닝 모델에서 layer는 연속되어 있는 데이터 프로세싱을 위한 여과기와 같습니다.
본 장에서는 완전 연결된(fully connected) 신경망 층인 Dense layer 2개를 사용합니다. 첫 번째 layer에서는 512개의 유닛(unit)과 활성화 함수 relu를 사용합니다. 두 번째 layer는 소프트맥스 분류 결과로 얻은 10개의 확률 점수가 들어있는 배열을 반환합니다. 각 점수는 해당 숫자 이미지가 10개의 숫자 클래스 중 하나에 속할 확률입니다.
from tensorflow import keras
from tensorflow.keras import layers
model = keras.Sequential([
layers.Dense(512, activation="relu"),
layers.Dense(10, activation="softmax")
])
컴파일 단계
신경망이 훈련하기 위해서는 컴파일을 해야 합니다. 컴파일 하기 위해서는 세 가지를 정해야합니다.
- 옵티마이저(optimizer): 성능을 향상시키기 위해 입력된 데이터를 기반으로 모델을 업데이트 하는 메커니즘
- 손실 함수(loss function): 훈련 데이터에서 모델의 성능을 측정하는 방법으로 모델이 옳은 방향으로 학습될 수 잇도록 도와줍니다.
- 훈련과 테스트 과정을 모니터링할 지표(metric): 모델의 성능을 숫자로 표현합니다.
model.compile(optimizer="rmsprop",
loss="sparse_categorical_crossentropy",
metrics=["accuracy"])optimizer, loss, metric에는 다양한 기법들이 있지만, 여기서 옵티마이저는 rmsprop, 손실 함수는 categorical crossentropy, metric으로는 accuracy를 사용합니다.
이미지 데이터 준비하기
훈련하기 전 데이터를 모델에 맞는 크기로 바꾸어야 합니다. 데이터의 모든 값을 0~1 사이로 스케일을 조정하고 float32 타입으로 바꿉니다. 이런 과정을 정규화(normalize)라고 합니다.
train_images = train_images.reshape((60000, 28 * 28))
train_images = train_images.astype("float32") / 255
test_images = test_images.reshape((10000, 28 * 28))
test_images = test_images.astype("float32") / 255
모델 훈련
fit() 메서드를 통해 모델을 훈련합니다. fit 메서드에는 fit(훈련 데이터, 훈련 레이블, 에폭, 배치 사이즈)가 매개 변수로 들어갑니다. 훈련 데이터와 훈련 레이블은 앞에서 정의한 훈련 데이터이고, 에폭은 전체 학습 데이터셋을 모델이 한 번 학습하는 것이고, 배치 사이즈는 한 번에 모델이 학습하는 데이터 샘플의 개수를 의미합니다.
model.fit(train_images, train_labels, epochs=5, batch_size=128)

위 결과는 훈련 데이터에 대한 결과입니다. 에폭 5회와 배치 사이즈 128의 결과, 훈련 데이터의 로스는 0.0378이고 accuracy는 0.9886입니다.
모델 예측
모델을 예측하기 위해서는 처음에 분리한 테스트 데이터를 사용합니다.
test_digits = test_images[0:10]
predictions = model.predict(test_digits)
predictions[0]
print(predictions[0].argmax()) # prediction[0]의 최댓값을 얻습니다
print(predictions[0][7]) # 확률을 확인합니다
print(test_labels[0]) # 테스트 레이블을 확인합니다
모델 평가
test_loss, test_acc = model.evaluate(test_images, test_labels)
print(f"테스트 정확도: {test_acc}")
정확도가 나왔습니다.
2.2 신경망을 위한 데이터 표현
텐서란?
텐서는 데이터를 위한 컨테이너(container)로 임의의 차원 개수를 가지는 행렬의 일반화된 모습입니다.
(텐서에서는 차원(dimension)을 종종 축(axis)이라고도 부릅니다.)
2.2.1 스칼라(랭크 - 0 텐서)
하나의 숫자만 담고 있는 텐서를 스칼라(scalar)라고 부릅니다. ndim 속성을 사용하면 넘파이 배열의 축(axis) 개수를 확인할 수 있습니다. 즉, 랭크(rank)를 확인할 수 있습니다.
import numpy as np
x = np.array(12)
x.ndim # 0 이 출력됩니다2.2.2 벡터(랭크 - 1 텐서)
숫자의 배열을 벡터(vector)라고 부릅니다. 벡터는 하나의 축을 가집니다.
x = np.array([12, 3, 6, 14, 7])
x # 1 이 출력됩니다2.2.3 행렬(랭크 - 2 텐서)
벡터의 배열은 행렬(matrix)라고 부릅니다. 행렬은 2개의 축(행과 열)이 있고, 숫자가 채워진 사각 격자라고 생각할 수 있습니다.
x = np.array([[5, 78, 2, 34, 0],
[6, 79, 3, 35, 1],
[7, 80, 4, 36, 2]])
x.ndim # 2가 출력됩니다
2.2.4 랭크 - 3 텐서와 더 높은 랭크의 텐서
x = np.array([[[5, 78, 2, 34, 0],
[6, 79, 3, 35, 1],
[7, 80, 4, 36, 2]],
[[5, 78, 2, 34, 0],
[6, 79, 3, 35, 1],
[7, 80, 4, 36, 2]],
[[5, 78, 2, 34, 0],
[6, 79, 3, 35, 1],
[7, 80, 4, 36, 2]]])
x.ndim 3 이 출력됩니다
2.2.5 핵심 속성
텐서는 3개의 속성으로 정의됩니다.
- 축의 개수(랭크): axis로 표현하고, ndim 속성으로 랭크를 확인할 수 있습니다.
- 크기(shape)
- 데이터 타입(dtype)
2.2.6 넘파이로 텐서 조작하기
2.1에서 불러온 MNIST 데이터의 훈련 이미지에서 10부터 100의 이미지를 슬라이싱 해보겠습니다.
my_slice = train_images[10:100]
my_slice.shape # (90, 28, 28) 출력
위와 같은 표현이지만 더 자세한 표기법은 다음과 같습니다.
my_slice = train_images[10:100, 0:28, 0:28]
my_slice.shape # (90, 28, 28) 출력콜론(:)은 전체 인덱스를 의미합니다.
2.2.7 배치 데이터
딥러닝 모델은 한 번에 전체 데이터셋을 처리하지 않습니다. 대신, 데이터를 작은 배치로 나누어 연산합니다.
2.2.8 텐서의 실제 사례
- 벡터 데이터: (sample, feature)로 이루어진 랭크-2 켄서. 각 샘플은 수치 속성(특성, feature)으로 구성된 벡터입니다.
- 시계열 데이터 또는 시퀀스 데이터: (sample, timesteps, features) 크기의 랭크-3 텐서입니다.
- 이미지 데이터: (samples, height, width, channels) 또는 (samples, channels , height, width) 크기의 랭크-4 텐서 입니다.
- 동영상 데이터: (samples, frames, height, width, channels) 또는 (samples, frames, channels , height, width) 크기의 랭크-5 텐서입니다.
2.2.9 벡터 데이터
대부분의 경우 해당됩니다. 하나의 데이터 포인트가 벡터로 인코딩되면 배치 데이터는 랭크-2 텐서로 인코딩 될 것입니다. 즉, 벡터의 배열입니다. 여기서 첫 번째 축은 샘플 축이고, 두 번재 축은 feature axis입니다.
2.2.10 시계열 데이터 또는 시퀀스 데이터
데이터에서 시간이 중요할 때는 시간 축을 포함하여 랭크-3 텐서로 저장됩니다. 각 샘플은 벡터의 시퀀스로 인코딩되므로 배치 데이터는 랭크-3 텐서로 인코딩될 것입니다.
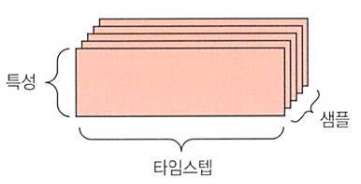
2.2.11 이미지 데이터
이미지는 전형적으로 높이, 너비, 컬러 채널의 3차원으로 이루어집니다. 흑백 이미지는 하나의 컬러 채널만 가지므로 랭크-2 텐서로 저장될 수 있지만, 관례상 이미지 텐서는 항상 랭크-3 텐서로 저장됩니다. 즉, 흑백 이미지의 경우 채널은 1입니다. 256x256 크기의 흑백 이미지에 대한 128개의 배치는 (128, 256, 256, 1) 크기의 텐서에 저장되고, 컬러 이미지에 대한 128개의 배치라면 (128, 256, 256, 3) 크기의 텐서에 저장됩니다.

2.2.12 비디오 데이터
비디오 데이터는 현실에서 랭크-5 텐서가 필요한 몇 안되는 데이터 중 하나입니다. 하나의 비디오는 프레임의 연속이고 각 프레임은 하나의 컬러 이미지입니다. 비디오는 (samples, frames, height, width, color_depth)의 랭크-5 텐서로 저장됩니다.
2.3 신경망의 톱니바퀴: 텐서 연산
Dense층을 쌓아서 모델을 생성. 케라스의 층은 다음과 같이 생성한다.
keras. layers. Dense(512, activation="relu")행렬을 입력으로 받고 입력 텐서의 새로운 표현인 또 다른 행렬을 반환하는 함수처럼 해석할 수 있다. (W는 행렬이고, b는 벡터이며 둘 모두 층의 속성이다.)
output = relu(dot(W, input) + b)3개의 텐서연산
• 입력 텐서와 텐서 W사이의 점곱(dot)
• 점곱으로 만들어진 행렬과 벡터b 사이의 덧셈(+)
• reLu(렐루) 연산. relu(x)는 max(x,0)
2.3.1 원소별 연산
단순한 원소별 연산
def naive_relu(x): assert len(x.shape) == 2 #X는 랭크-2 넘파이 배열입니다. x = x.copy() #입력텐서 자체를 바꾸지 않도록 복사합니다. for i in range(x.shape[0]): for j in range(x.shape[1]): x|i, j] = max(x[i, j], 0) return x덧셈도 동일하다.
def naive_add(x, y): assert len(x.shape) == 2 # x와y는 랭크-2 넘파이 배열입니다. assert x. shape == y.shape x = x.copy() # 입력 텐서 자체를 바꾸지 않도록 복사합니다. for i in range(x.shape[0]): for j in range(x. shape[11): x[i, j] += y[i, j] return x같은 원리로 원소별 곱셈, 뺄셈 등도 할 수 있다.
사실 넘파이 배열을 다룰 때 최적화된 넘파이 내장 함수로 이런 연산 처리를 할 수 있다.
넘파이 내장 함수를 사용하면 엄청난 속도로 연산을 처리할 수 있다.
import numpy as npz = X + Y #원소별 덧셈
z = np.maximum(z, 0.) #원소별 렐루 함수2.3.2 브로드캐스팅
브로드캐스팅은 두 단계로 이루어진다.
-
큰 텐서의 ndim에 맞도록 작은 텐서에 (브로드캐스팅 축이라고 부르는) 축이 추가된다.
-
작은 텐서가 새 축을 따라서 큰 텐서의 크기에 맞도록 반복된다.
예를 들어 x의 크기는 (32, 10)이고 y의 크기는 (10,)라고 가정합시다.
import numpy as np
X = np.random.random((32, 10)) #X는크기가(32,10)인 랜덤한 행렬이다.
y = np.random.random((10,)) #y는크기가(10,)인 랜덤한 벡터이다.먼저 y에 비어있는 첫번째 축을 추가하여 크기를 (1, 10)으로 만든다. 그런 다음 y를 이 축에 32번반복하면서 Y의 크기는 (32,10)이 된다. 여기에서 Y[i,:]== y for i in range(0, 32)이다.
y = np.expand_dims(y, axis=0) #이제 y의 크기는(1, 10)이다.
Y = np.concatenate([y] * 32, axis=0) #축 0을 따라 y를 32번 반복하여 크기가 (32, 10)인 Y를 얻는다.새로운 축을 따라 벡터가 32번 반복된다. 이때 브로드캐스팅은 a부터 n-1까지의 축에 자동으로 일어난다.
def naive_add_matrix_and_vector(x, y): assert len(x.shape) == 2 #x는 랭크-2 넘파이 배열
assert len(y.shape) == 1 #y는 넘파이 벡터
assert x.shape[1] == y.shape[0]
x = x.copy() #입력 텐서 자체를 바꾸지 않도록 복사한다.
for i in range(x. shape[0]):
for j in range(x. shape[1]):
x[i, j] += y[j]
return x크기가 다른 두 텐서에 브로드캐스팅으로 원소별 maximum 연산을 적용하는 방법이다.
import numpy as np
x = np.random.random((64, 3,32, 10)) #x는(64,3,32,10) 크기의 랜덤 텐서
y = np.random.random((32, 10)) #y는(32,10) 크기의 랜덤 텐서
z = пр.maximum(x, y) #출력 z크기는 x와 동일하게 (64,3,32,10)이다.2.3.3 텐서 곱셈
x = np.random.random((32,))
y = np.random.random((32,))
z = np.dot(x, y)두 벡터의 점곱은 스칼라가 되므로 원소 개수가 같은 벡터끼리 점곱이 가능하다.
def naive_vector_dot(x, y):
assert len(x.shape) == 1
assert len(y.shape) == 1 #x와 y는 넘파이 벡터이다.
assert X.shape[0] == y.shape[0]
z = 0.
for i in range(x.shape[0]):
z += x[i] * y[i]
return z2.3.4 텐서 크기 변환

2.3.5 텐서 연산의 기하학적 해석
일반적으로 이동, 회전, 크기 변경, 기울이기 등과 같은 기본적인 기하학적 연산은 텐서 연산으로 표현할 수 있다.
-
이동 : 한 점에 벡터를 더하면 고정된 방향으로 고정된 양만큼 점을 이동시킨다. 점 집합에 적용하면 이를 이동이라 부름
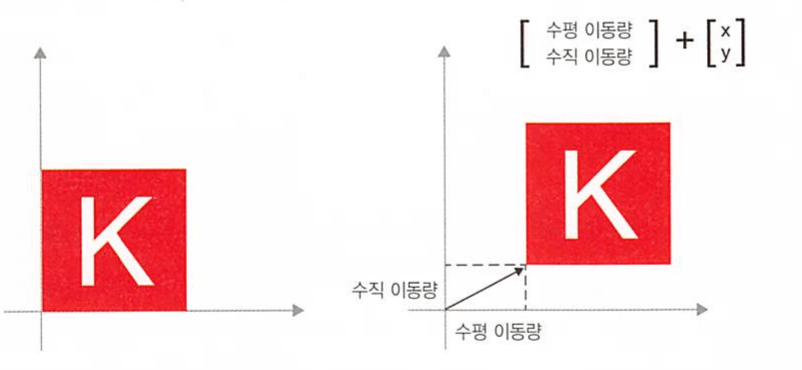
-
회전 : 각도 theta만큼 2D 벡터를 반시계 방향 회전한 결과는 2x2 행렬 R= [[cos(theta), - sin(thet a)], [ sin(theta), cos(theta)]] 와 점곱하여 얻을수 있다.
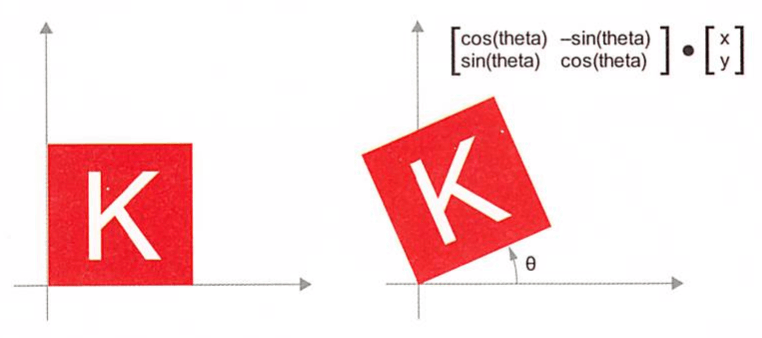
-
크기 변경 : 2X2행렬 S=[[horizontal_factor,0l, [0, vertical_factor]]와 점곱하여 수직과 수평 방향으로 크기를 변경시킨다. 이런 행렬을 ‘대각 행렬’이라고도 부른다.
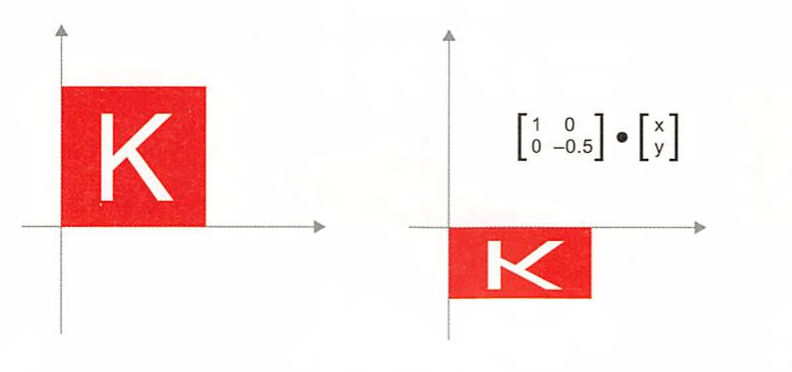
-
선형 변환 : 임의의 행렬과 점곱하면 선형 변환이 수행된다.
-
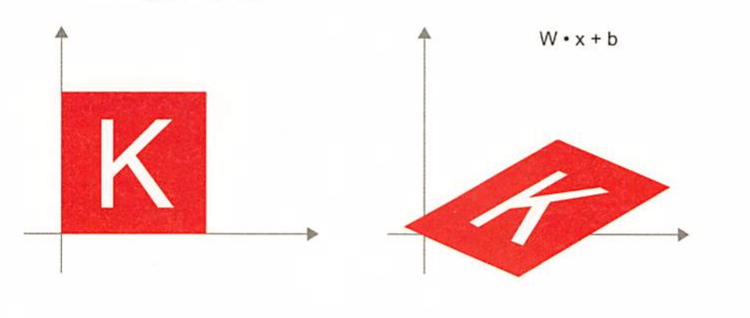
아핀 변환 : 선형 변환과 (벡터를 더해 얻는) 이동의 조합이다. 활성화 함수를 사용하지 않는 Dense층은 일종의 아핀 변환 층이다.
-
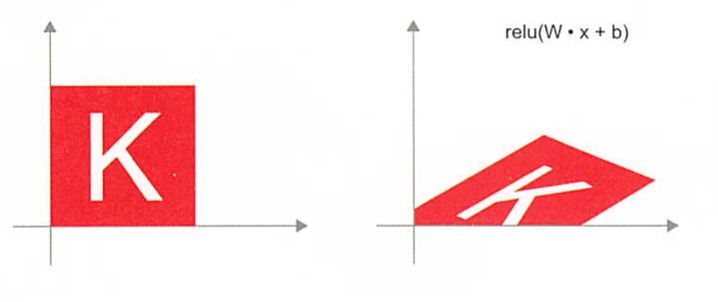
relu 활성화 함수를 사용하는 Dense 층 : 아핀 변환의 중요한 성질 하나는 여러 아핀 변환을 반복해서 적용해도 결국 하나의 아핀 변환이 된다는 것이다. affine2(affine1(x)) = W2 x + b1) + b2 = (W2 x + (W2 * b1 + b2) 에서 선형 변환 부분이 행렬 W2 * W1이고, 이동 부분이 벡터 W2 * b1 + b2인 하나의 아핀 변환이다. 결국 활성화 함수 없이 Dense층으로만 구성된 다층 신경망은 하나의 Dense층과 같다.(뭔소리야)
2.3.6 딥러닝의 기하학적 해석
신경망은 전체적으로 텐서 연산의 연결로 구성된 것이고, 모든 텐서 연산은 입력 데이터의 간단한 기하학적 변환이다. 단순한 단계들이 길게 이어져 구현된 신경망을 고차원 공간에서 매우 복잡한 기하학적 변환을 하는 것으로 해석할 수 있다.
2.4 신경망의 예측: 그레이디언트 기반 최적화
신경망은 입력 데이터와 가중치(weight)를 사용하여 출력(output)을 생성합니다.
output = relu(dot(W, input) + b) →신경망의 기본수식
(W : 가중치(또는 커널), b : 편향(bias) - 이들은 학습 가능한 파라미터) 이 과정은 데이터를 네트워크의 가중치와 결합하여 출력을 생성하는 것이다.
<훈련 루프(training loop)의 4단계> ①훈련 세트에서 배치를 추출하여 실제 타깃 y_true와 비교하여 모델의 예측을 생성합니다. ②모델이 예측한 값 y_pred와 실제 값 y_true 사이의 손실을 계산합니다. ③손실을 감소시키기 위해 역전파(backward pass) 단계를 수행하여 가중치를 조정합니다. ④이러한 과정을 반복하여 모델의 모든 가중치를 최적화합니다.
신경망은 실제 타깃 y_true와 예측값 y_pred 사이의 오차를 최소화하는 방향으로 가중치를 조정합니다. 모델의 출력은 가중치 W, 입력 input, 편향 b를 사용하여 계산되며, 이 과정에서 각 데이터 포인트가 신경망을 통과할 때마다 손실을 발생시킵니다.
손실 함수를 최소화하기 위해, 신경망은 손실이 가장 낮아지는 방향으로 가중치를 조정해야 합니다. 이를 위해 그레이디언트(기울기)를 계산하고, 이 그레이디언트를 사용하여 가중치를 업데이트하는 과정이 반복됩니다. 그레이디언트 : 손실 함수의 현재 가중치에 대한 미분값 예) 신경망의 각 가중치에 대한 손실 함수의 그레이디언트가 계산된 후, 그 값에 학습률(learning rate)을 곱하여 가중치를 업데이트한다.
그레이디언트가 양수일 경우 가중치를 감소시키고, 음수일 경우 가중치를 증가시켜 손실을 줄입니다. 이 과정을 통해 모델은 데이터의 구조를 배우고, 새로운 데이터에 대해 정확한 예측을 할 수 있게 됩니다.
그레이디언트 기반 최적화는 학습률이 중요한 역할을 합니다. 모델은 점차 최적의 가중치를 찾아가며 성능을 개선합니다.
2.4.2 테일러 급수의 도함수: 그레이디언트
다변수 함수에서는 각 변수에 대해 편도함수(partial derivative)를 계산하여 그레이디언트를 구합니다. 그레이디언트는 벡터로서 각 변수에 따른 함수의 기울기를 나타내며, 함수의 가장 가파른 상승 경로를 나타냅니다.
손실을 통해 신경망은 예측 y_pred를 실제 타깃 y_true에 점점 더 가까워지도록 가중치 W를 조정합니다. 손실 함수 loss(y_pred, y_true)를 W에 대해 미분하여 그레이디언트를 구하고, 이를 사용하여 가중치를 업데이트합니다.
그레이디언트를 구하는 과정에서 편미분(partial derivative)이 사용되며, 이는 각 가중치 w[i]에 대한 손실 함수의 변화율을 나타냅니다. 특정 가중치 w[i]에 대한 손실 함수의 편미분은 grad(loss_value, w)[i]로 표현됩니다. 이는 함수 f(w) = loss_value의 편미분으로, w[i]만 변화할 때 손실 값의 변화를 나타냅니다. 이러한 방식으로 각 가중치의 그레이디언트를 구하고, 이를 사용하여 네트워크를 최적화합니다.
W1 = W0 - step * grad(f(W0), W0) →새로운 가중치를 계산하기
(가중치 W0에서의 손실 함수 값 loss_value를 계산한 후, W0에 대한 손실 함수의 그레이디언트 grad(loss_value, W0)를 통해 가중치를 어떻게 조정할지 결정한다. step : 학습률로, 가중치 조정의 크기를 결정한다.)
2.4.3 확률적 경사 하강법
학습률 : 네트워크가 얼마나 빠르게 학습할지를 결정하는 중요한 요소입니다. 학습률이 너무 높으면 네트워크가 최적화 과정에서 불안정해질 수 있으며, 너무 낮으면 학습 속도가 느려질 수 있습니다. 학습률이 너무 크면 최적화 과정에서 지역 최소값에 빠질 수 있으며, 너무 작으면 학습이 느려져 전역 최소값에 도달하는 데 더 많은 시간이 소요될 수 있습니다. 그래디언트 : 주어진 가중치에 대한 손실 함수의 변화율을 나타낸다.
<그래디언트 기반 최적화 방법> 1.실제 타깃 y_true와 예측 y_pred 사이의 손실을 계산합니다. 2.계산된 손실을 바탕으로 예측 y_pred를 개선하기 위해 가중치 W를 업데이트합니다. 3.이러한 과정을 반복하여 신경망이 데이터의 구조를 배우고, 이를 기반으로 예측 성능을 향상시킵니다.
grad(f(W), W) = 0 → 손실함수의 최소값
W_new = W_old - learning_rate * gradient → 가중치 업데이트
SGD (확률적 그레디언트 하강법) : 무작위로 선택된 미니 배치를 사용하여 그레이디언트를 계산하고 가중치를 업데이트한다. 전체 데이터셋 대신 미니 배치를 사용하여 계산 효율성을 높이고 메모리 사용량을 줄인다.
최적화 방법 : 신경망이 빠르게 최적의 가중치를 찾아가도록 돕는다. 모멘텀 - 가중치 업데이트 시 이전 그레디언트가 미치는 영향을 고려해 가중치의 업데이트를 더 부드럽고 안정적으로 만든다. 특정한 최적화방법들은 지역 최소값(local minimum)에 갇히지 않고 전역 최소값(global minimum)을 찾는 데 도움을 준다. 이는 최적화 과정에서 발생할 수 있는 잠재적인 문제점을 피하고 효과적으로 최적의 솔루션으로 이동하는 데 도움이 됩니다.
--실제 코드 예시 모멘텀을 적용한 가중치 업데이트 방식이 제시되어 있음 현재 가중치, 손실 및 그라디언트를 계산한 후, 모멘텀과 이전 속도를 고려하여 새로운 가중치를 계산하는 방식 가중치는 현재의 그레이디언트와 모멘텀에 의해 결정된 속도를 바탕으로 업데이트된다.
2.4.4 도함수 연결 : 역전파 알고리즘
역전파 : 네트워크의 출력층에서부터 입력층으로 거슬러 올라가면서 가중치를 조정한다. 연쇄법칙을 사용해 각 레이어의 가중치에 대한 손실함수의 그라디언트를 계산한다.
연쇄법칙 : 복합함수의 도함수를 구할 때 내부함수의 도함수와 외부함수의 도함수를 곱하여 구하는 방법이다.
계산 그래프 (computation graph) : 신경망의 데이터 흐름과 연산을 시각화하는 데 도움을 주는 도구이다. 각 노드가 특정 연산을 나타내고 엣지가 데이터의 흐름을 나타내는 방식으로 구성된다. 이를 통해, 더 복잡한 신경망에서도 자동 미분을 통해 그라디언트를 효율적으로 계산할 수 있다.
<TensorFlow를 사용하여 그라디언트를 계산하는 방법>
import tensorflow as tf
#스칼라 값으로 가중치 변수를 생성합니다. 초기 값은 0.0입니다.
x = tf.Variable(0.0)
#GradientTape 컨텍스트를 사용하여 연산을 기록합니다.
with tf.GradientTape() as tape:
# y는 x에 대한 선형 함수입니다. y = 2x + 3
y = 2 * x + 3
#tape.gradient()를 사용하여 y의 x에 대한 그라디언트를 계산합니다.
#이 연산은 y가 x에 얼마나 민감하게 반응하는지 측정합니다.
grad_of_y_wrt_x = tape.gradient(y, x)
#GradientTape는 다양한 텐서 연산에 대한 그라디언트를 자동으로 계산할 수 있습니다.
#여기에서는 2x2 행렬을 가중치로 사용하고 모든 요소를 0으로 초기화합니다.
w = tf.Variable(tf.zeros((2, 2)))
#편향 변수도 생성하고, 이 또한 2x2 행렬로 모든 요소를 0으로 초기화합니다.
b = tf.Variable(tf.zeros((2,)))
#입력 데이터를 랜덤하게 생성합니다. 이것은 2x2 행렬입니다.
x = tf.random.uniform((2, 2))
#다시 GradientTape 컨텍스트를 사용하여 연산을 기록합니다.
with tf.GradientTape() as tape:
# 행렬 연산을 사용하여 y를 계산합니다. y = x * w + b
# tf.matmul은 행렬 곱셈을 의미하며, 여기서는 입력 x와 가중치 w의 행렬 곱을 계산합니다.
y = tf.matmul(x, w) + b
#tape.gradient()를 사용하여 y의 w와 b에 대한 그라디언트를 계산합니다.
#이 연산은 y가 w와 b에 대해 얼마나 민감하게 반응하는지 측정합니다.
grad_of_y_wrt_w_and_b = tape.gradient(y, [w, b]) 2.5 첫 번째 예제 다시 살펴보기
-
층이 서로 연결되어 모델을 구성.
-
모델은 입력 데이터를 예측으로 매핑.
-
손실 함수가 예측값과 타깃을 비교하여 손실 값을 생성
-
모델의 예측이 기대한 것에 얼마나 잘 맞는지 측정
-
손실 값을 옵티마이저를 통해 사용하여 모델의 가중치를 업데이트
import tensorflow as tf
# NaiveDense 클래스 정의
class NaiveDese:
def __init__(self, input_size, output_size, activation):
self.activation = activation
w_shape = (input_size, output_size)
w_initial_value = tf.random.uniform(w_shape, minval = 0, maxval = 1e-1)
self.W = tf.Variable(w_initial_value)
b_shape = (output_size,)
b_initial_value = tf.zeros(b_shape)
self.b = tf.Variable(b_initial_value)
def __call__(self, inputs):
return self.activation(tf.matmul(inputs, self.W) + self.b)
@property
def weights(self):
return [self.W, self.b]# 단순한 Sequential 클래스
class NaiveSequential:
def __init__(self, layers):
self.layers = layers
def __call__(self, inputs):
x = inputs
for layer in self.layers:
x = layer(x)
return x
@property
def weights(self):
weights = []
for layer in self.layers:
weights += layer.weights
return weights-
위의 두 클래스를 이용하여 케라스와 유사한 모델을 만들 수 있습니다.
# 모델 구성
model = NaiveSequential([
NaiveDense(input_size=28 * 28, output_size=512, activation=tf.nn.relu),
NaiveDense(input_size=512, output_size=10, activation=tf.nn.softmax)
])
assert len(model.weights) == 4# 배치 제네레이터
# MNIST 데이터를 미니 배치로 순회하는 방법
import math
class BatchGenerator:
def __init__(self, images, labels, batch_size = 128):
assert len(images) == len(labels)
self.index = 0
self.images = images
self.labels = labels
self.batch_size = batch_size
self.num_batches = math.ceil(len(images) / batch_size)
def next(self):
images = self.images[self.index : self.index + self.batch_size]
labels = self.labels[self.index : self.index + self.batch_size]
self.index += self.batch_size
return images, labels
2.5.2 훈련 스텝 실행하기
-
배치에 있는 이미지에 대해 모델의 예측을 계산
-
실제 레이블일 사용하여 예측의 손실 값을 계산
-
모델 가중치에 대한 손실의 그레디언트를 계산
-
그레디언트의 반대 방향으로 가중치를 조금 이동
# 위의 그레디언트를 계산하기 위해 GradientTape 객체를 사용
import tensorflow as tf
def one_training_step(model, images_batch, labels_batch):
# TensorFlow의 GradientTape 컨텍스트를 열어 자동 미분을 위한 환경을 설정합니다.
with tf.GradientTape() as tape:
# 모델을 사용하여 입력 배치에 대한 예측을 수행합니다.
predictions = model(images_batch)
# 손실 함수를 사용하여 실제 레이블과 예측 간의 손실을 계산합니다.
# 여기서는 희소 범주형 크로스 엔트로피 손실 함수를 사용합니다.
per_sample_losses = tf.keras.losses.sparse_categorical_crossentropy(
labels_batch, predictions)
# 배치에 대한 평균 손실을 계산합니다.
average_loss = tf.reduce_mean(per_sample_losses)
# GradientTape를 사용하여 모델의 가중치에 대한 손실의 그레이디언트를 계산합니다.
gradients = tape.gradient(average_loss, model.weights)
# 계산된 그레이디언트를 사용하여 모델의 가중치를 업데이트합니다.
# 이 함수는 외부에서 정의되어야 합니다.
update_weights(gradients, model.weights)
# 평균 손실을 반환합니다. 이 값은 훈련 과정을 모니터링하는 데 사용될 수 있습니다.
return average_loss-
가중치 업데이트 단계의 목적은 배치의 손실을 감소시키기 위한 방향으로 가중치를 조금 이동하는 것, 이동의 크기는 '학습률'에 의해 결정 됨.
learning_rate = 1e-3
def updata_weights(gradients, weights):
for g, w in zip(gradients, weights):
w.assign_sub(g * learning_rate)-
실제로는 Optimizer 인스턴스를 사용한다.
optimizer = optimizers.SGD(learning_rate=1e-3)
def update_weights(gradients, weights):
optimizer.apply_gradients(zip(gradients, weights))
2.5.3 전체 훈련 루프
def fit(model, images, labels, epochs, batch_size=128):
for epoch_counter in range(epochs):
# 현재 에포크 번호를 출력합니다.
print(f"Epoch {epoch_counter}")
# 배치 생성기를 초기화합니다. 이는 이미지와 레이블을 미니 배치로 분할하는 데 사용됩니다.
batch_generator = BatchGenerator(images, labels, batch_size)
# 생성된 각 배치에 대해 반복을 수행합니다.
for batch_counter in range(batch_generator.num_batches):
# 다음 미니 배치를 생성합니다.
images_batch, labels_batch = batch_generator.next()
# 한 훈련 단계를 수행하고, 이때 발생한 평균 손실을 계산합니다.
loss = one_training_step(model, images_batch, labels_batch)
# 정기적으로 현재 배치 번호와 평균 손실을 출력합니다.
if batch_counter % 100 == 0:
print(f"Batch {batch_counter}: Loss {loss:.2f}")-
위의 fit 함수는 각 에포크마다 모델을 전체 데이터셋에 대해 여러 번 훈련시킵니다.
-
각 훈련 단계에서는 one_training_step 함수를 사용하여 모델의 가중치를 업데이트합니다.
-
BatchGenerator 클래스는 전체 데이터셋을 작은 배치로 분할하여 모델의 훈련을 더 효율적으로 만듭니다.
# 함수 테스트
from tensorflow.keras.datasets import mnist
# MNIST 데이터셋을 로드합니다. 여기서는 훈련 데이터는 사용하지 않습니다.
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
# 이미지를 전처리합니다. 이미지를 평탄화하고, 0과 1 사이의 값으로 정규화합니다.
train_images = train_images.reshape((60000, 28 * 28))
train_images = train_images.astype('float32') / 255
test_images = test_images.reshape((10000, 28 * 28))
test_images = test_images.astype("float32") / 255
fit (model, train_images, train_labels, epochs = 10, batch_size = 128)2.5.4 모델 평가하기
테스트 이미지에 대한 예측에 argmax 함수를 적용하고, 예상 레이블과 비교하여 모델을 평가합니다.
# 훈련된 모델로 테스트 데이터에 대한 예측을 수행합니다.
predictions = model(test_images)
# 예측 결과를 numpy 배열로 변환합니다.
predictions = predictions.numpy()
# 각 예측에 대해 가장 높은 확률을 가진 클래스를 선택합니다.
predicted_labels = np.argmax(predictions, axis=1)
# 예측된 레이블과 실제 테스트 레이블을 비교하여 정확도를 계산합니다.
matches = predicted_labels == test_labels
print(f"Accuracy: {matches.mean():.2f}")2.6 요약
-
텐서
-
텐서는 데이터를 위한 컨테이너로, 주로 수치형 데이터를 저장하기 위한 것입니다.
-
텐서는 배열이나 행렬과 유사하며, 데이터 타입(dtype), 차원의 수(ndim), 모양(shape) 등을 특징으로 합니다.
-
머신 러닝에서는 이러한 텐서를 이용해 데이터를 조작하고 계산을 수행합니다.
-
-
모델과 프레임워크
-
딥러닝 모델을 구축하기 위해 텐서를 매개변수로 받는 연산을 연결합니다.
-
모델의 학습은 이러한 연산을 통해 최적화됩니다.
-
-
학습
-
학습은 데이터에 숨겨진 표현을 학습하기 위해 모델의 가중치를 조정하는 과정입니다.
-
이를 위해 데이터와 타깃이 주어질 때 모델의 가중치가 최소화되는 방향으로 조정됩니다.
-
-
데이터 표현
-
데이터를 표현하는 방식에는 다양한 형태가 있으며, 이러한 데이터 표현에 대한 이해는 딥러닝 모델을 제대로 이해하고 작업하는 데 필요합니다.
-
-
신경망의 작동
-
신경망은 파라미터와 배치 데이터를 그레이디언트 값에 매핑하는 그레이디언트 함수를 사용합니다.
-
이 과정은 미분 가능한 모든 텐서 연산과 연쇄 법칙에 기반하여 역전파를 통해 수행됩니다.
-
-
손실과 옵티마이저
-
핵심적인 두 가지 개념인 손실과 옵티마이저는 모델을 훈련하기 전에 정의되어야 합니다.
-
손실은 문제를 해결하는데 있어 모델의 성공을 측정하는데 사용되며, 옵티마이저는 손실에 대한 그레이디언트가 파라미터를 업데이트하는 방식을 정의합니다.
-
-
손실 최소화
-
손실을 최소화하는 것은 학습하는 동안 최소화해야 할 양이며, 이를 통해 모델의 성능을 측정할 때 사용됩니다.
-
-
옵티마이저
-
옵티마이저는 손실에 대한 그레이디언트가 파라미터를 어떻게 업데이트할지 정의하는 중요한 구성 요소입니다.
-
대표적인 옵티마이저로는 RMSProp과 SGD(확률적 경사 하강법)가 있습니다.
-
'AI > 인공지능 기초' 카테고리의 다른 글
| 케라스 창시장에게 배우는 딥러닝 5장 (0) | 2023.12.12 |
|---|---|
| 케라스 창시장에게 배우는 딥러닝 3장 (0) | 2023.12.08 |
| 모델 저장과 콜백 (1) | 2023.12.06 |
| 딥러닝 모델 학습 (0) | 2023.12.06 |
| 딥러닝 구조와 모델 (0) | 2023.12.06 |



