| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- Dehaze
- 자바 프로젝트
- 자바
- 로스트아크
- 인공지능 깃 버전관리
- 의료 ai 대학원 월급
- 딥러닝 실험 깃 버전관리
- 대학원 월급
- 인공지능
- 영화 api
- 디자인 패턴
- 딥러닝
- DCP
- 자바 영화 api
- MLP
- 활성화 함수
- 정규화
- 경사하강법
- 통계학
- 코딩테스트
- C# 프로젝트
- API
- 백준
- 파이썬 경사하강법
- 파이썬
- 디자인패턴
- python
- pandas
- 머신러닝
- 대학원 급여
- Today
- Total
대학원 일기
딥러닝 들여다보기 본문
신경망
머신러닝/딥러닝 과학자들도 자연에서 답을 찾으려 노력했고, 우리 뇌 속의 신경망 구조에 착안해서 퍼셉트론(Perceptron)이라는 형태를 제안하며 이를 연결한 형태를 인공신경망(Artificial Neural Network)이라고 부르기 시작했습니다.
입력층(input layer), 최종 출력값이 있는 출력층(output layer), 그리고 그 사이에 있는 층인 은닉층(hidden layer)이 있습니다. 보통 입력층과 출력층 사이에 몇 개의 층이 존재하든 모두 은닉층이라고 부릅니다.
레이어 개수를 셀 때는 노드와 노드 사이의 연결하는 부분이 몇 개 존재하는지 세면 보다 쉽게 알 수 있습니다.
인공신경망 중에서도 위의 이미지처럼 2개 이상의 레이어를 쌓아서 만든 것을 보통 다층 퍼셉트론(Multi-Layer Perceptron; MLP) 이라고 부릅니다. 그리고 입력층, 출력층을 제외한 은닉층이 많아지면 많아질수록 인공신경망이
DEEP 해졌다고 이야기합니다. 우리가 지금 알아보려고 하는 딥러닝이 바로 이 인공신경망이 DEEP 해졌다는 뜻에서 나온 단어입니다. 그래서 우리가 하려는 딥러닝은 충분히 깊은 인공신경망을 활용하며 이를 보통 다른 단어로 DNN(Deep Neural Network) 라고 부릅니다.
Fully-Connnected Nerual Network는 서로 다른 층에 위치한 노드 간에는 연결 관계가 존재하지 않으며, 인접한 층에 위치한 모든 노드-노드 쌍에 대해 연결이 존재한다는 의미를 내포합니다.
앞에서 설명한 입력층-은닉층, 은닉층-출력층 사이에는 사실 각각 행렬(Matrix)이 존재합니다.
예를 들어 입력값이 100개, 은닉 노드가 20개라면 입력층-은닉층의 모든 노드-노드 쌍에 대해 연결이 존재하므로 사실
입력층-은닉층 사이에는 100x20 의 형태를 가진 행렬이 존재합니다. 똑같이, MNIST 데이터처럼 10개의 클래스를 맞추는 문제를 풀기 위해 출력층이 10개의 노드를 가진다면 은닉층-출력층 사이에는 20x10 의 형태를 가진 행렬이 존재하게 됩니다.
이 행렬들을 Parameter 혹은 Weight라고 부릅니다. 두 단어는 보통 같은 뜻으로 사용되지만, 실제로 Parameter에는 위의 참고 자료에서 다룬 bias 노드도 포함된다는 점만 유의해 주세요.
이때 인접한 레이어 사이에는 아래와 같은 관계가 성립합니다.
$ y=W * X+b$
weight_init_std = 0.1
input_size = 784
hidden_size=50
# 인접 레이어간 관계를 나타내는 파라미터 W를 생성하고 random 초기화
W1 = weight_init_std * np.random.randn(input_size, hidden_size)
# 바이어스 파라미터 b를 생성하고 Zero로 초기화
b1 = np.zeros(hidden_size)
# 은닉층 출력
a1 = np.dot(X, W1) + b1활성 함수
활성화 함수는 보통 비선형 함수를 사용하는데 이 비선형 함수를 MLP 안에 포함시키면서 모델의 표현력이 좋아지게 됩니다. (정확히는 레이어 사이에 이 비선형 함수가 포함되지 않은 MLP는 한 개의 레이어로 이루어진 모델과 수학적으로 다른 점이 없습니다.)
sigmoid
$ σ(x)=\frac{1}{1+e^{−x}}$
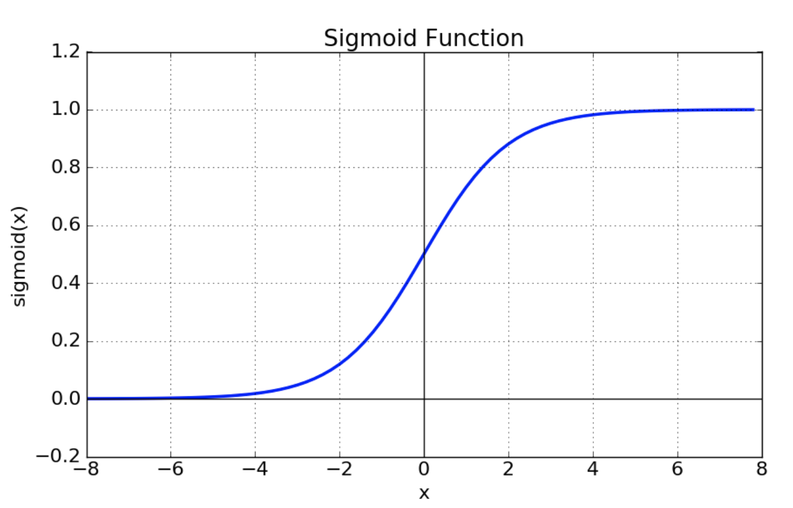
def sigmoid(x):
return 1 / (1 + np.exp(-x))-
vanishing gradient 현상이 발생한다.
-
exp 함수 사용 시 비용이 크다.
tanh
$ tanh(x) = \frac{e^x-e^{-x}}{e^x+e^{-x}}$
-
tanh 함수는 함수의 중심값을 0으로 옮겨 sigmoid의 최적화 과정이 느려지는 문제를 해결.
-
vanishing gradient 문제 존재.

ReLU
$f(x) = max(0, x)$
-
sigmoid, tanh 함수에 비해 학습이 빠름.
-
연산 비용이 크지 않고, 구현이 매우 간단하다.

어떤 함수를 사용할까
-
우선 가장 많이 사용되는 함수는 ReLU이다. 간단하고 사용이 쉽기 때문에 우선적으로 ReLU를 사용한다.
-
ReLU를 사용한 이후 Leakly ReLU등 ReLU계열의 다른 함수도 사용 해본다.
-
sigmoid의 경우에는 사용하지 않도록 한다.
-
tanh의 경우도 큰 성능은 나오지 않는다.
SoftMax
def softmax(x):
if x.ndim == 2:
x = x.T
x = x - np.max(x, axis=0)
y = np.exp(x) / np.sum(np.exp(x), axis=0)
return y.T
x = x - np.max(x) # 오버플로 대책
return np.exp(x) / np.sum(np.exp(x))
y_hat = softmax(a2)
손실 함수
비선형 활성화 함수를 가진 여러 개의 은닉층을 거친 다음 신호 정보들은 출력층으로 전달됩니다. 이때 우리가 원하는 정답과 전달된 신호 정보들 사이의 차이를 계산하고, 이 차이를 줄이기 위해 각 파라미터들을 조정하는 것이 딥러닝의 전체적인 학습 흐름입니다. 이 차이를 구하는 데 사용되는 함수는 손실함수(Loss function) 또는 비용함수(Cost function)라고 부릅니다.
평균 제곱 오차
$MSE = \dfrac {1} {n} \sum_{i=1}^{n} (Y_i - \hat {Y_i})^2$
Cross Entropy
두 확률분포 사이의 유사도가 클수록 작아지는 값입니다. 아직 별로 학습되지 않은 현재의 모델이 출력하는 softmax 값
$\hat y$은 10개의 숫자 각각의 확률이 대부분 0.1 근처를 오가는 정도입니다.
모델을 학습하게 되면, \hat y이 점점 정답에 가까워지게 됩니다.
$E = - \sum_{i=1}^{n} t_i \log{y_i}$ (ti, yi는 각각 정답 벡터와 모델의 예측값 벡터 \hat y의 원소들)
# 정답 라벨을 One-hot 인코딩하는 함수
def _change_one_hot_label(X, num_category):
T = np.zeros((X.size, num_category))
for idx, row in enumerate(T):
row[X[idx]] = 1
return T
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
# 훈련 데이터가 원-핫 벡터라면 정답 레이블의 인덱스로 반환
if t.size == y.size:
t = t.argmax(axis=1)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), t])) / batch_size
Loss = cross_entropy_error(y_hat, t)
Loss경사하강법
오차를 줄이기 위한 방법, 각 단계에서의 기울기를 구해서 해당 기울기가 가리키는 방향으로 이동하는 방법.
학습률(learning rate) 이라는 개념을 도입해 기울기 값과 이 학습률을 곱한 만큼만 이동.
# softmax값의 출력으로 Loss를 미분한 값
batch_num = y_hat.shape[0]
dy = (y_hat - t) / batch_num
print(dy.shape)
dy여기서 $dy = \frac { \partial Loss}{\partial y}$, 일단 dy가 구해지면 다른 기울기들은 chain-rule로 쉽게 구해집니다.
중간에 sigmoid가 한번 사용되었으므로, 활성화함수에 대한 gradient도 고려되어야 합니다.
def affine_layer_backward(dy, cache):
X, W, b = cache
dX = np.dot(dy, W.T)
dW = np.dot(X.T, dy)
db = np.sum(dy, axis=0)
return dX, dW, db # dX는 사용하진 않음.
learning_rate = 0.1
def update_params(W1, b1, W2, b2, dW1, db1, dW2, db2, learning_rate):
W1 = W1 - learning_rate*dW1
b1 = b1 - learning_rate*db1
W2 = W2 - learning_rate*dW2
b2 = b2 - learning_rate*db2
return W1, b1, W2, b2# 파라미터 초기화
W1 = weight_init_std * np.random.randn(input_size, hidden_size)
b1 = np.zeros(hidden_size)
W2 = weight_init_std * np.random.randn(hidden_size, output_size)
b2 = np.zeros(output_size)
# Forward Propagation
a1, cache1 = affine_layer_forward(X, W1, b1)
z1 = sigmoid(a1)
a2, cache2 = affine_layer_forward(z1, W2, b2)
# 추론과 오차(Loss) 계산
y_hat = softmax(a2)
t = _change_one_hot_label(Y_digit, 10) # 정답 One-hot 인코딩
Loss = cross_entropy_error(y_hat, t)
print(y_hat)
print(t)
print('Loss: ', Loss)
# Backward Propagation
dy = (y_hat - t) / X.shape[0]
dz1, dW2, db2 = affine_layer_backward(dy, cache2)
da1 = sigmoid_grad(a1) * dz1
dX, dW1, db1 = affine_layer_backward(da1, cache1)
# 경사하강법을 통한 파라미터 업데이트
learning_rate = 0.1
W1, b1, W2, b2 = update_params(W1, b1, W2, b2, dW1, db1, dW2, db2, learning_rate)def predict(W1, b1, W2, b2, X):
a1 = np.dot(X, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
y = softmax(a2)
return ydef accuracy(W1, b1, W2, b2, x, y):
y_hat = predict(W1, b1, W2, b2, x)
y_hat = np.argmax(y_hat, axis=1)
accuracy = np.sum(y_hat == y) / float(x.shape[0])
return accuracy
'AI > 인공지능 기초' 카테고리의 다른 글
| Deep Learning Layer: Linear Layer (1) | 2023.11.20 |
|---|---|
| Embedding, Recurrent Layer (0) | 2023.11.13 |
| MLP(Multi Layer Perceptron) 과정 (1) | 2023.11.13 |
| 전처리 기법: 원-핫 인코딩(One-Hot Encoding), 구간화(Data bining) (0) | 2023.11.12 |
| 전처리 기법: 정규화(Normalization) (1) | 2023.11.12 |



